Location Planning and Networks
The competitive position and economic success of an enterprise depends essentially on factors which are directly constrained by the facility locations and the internal locations.
Therefore the facility location decisions are highly important for the viability of the business though they are highly inflexible. Inevitably the facility location decision has to be made for long time horizons into the future, assigning it to strategic corporate planning.
The loss incurred by disadvantageous locations needs to be compensated by special efforts and endanger the rentability of the enterprise.
As a conclusion facility location can not only be seen as part of a strategic logistics planning but at the same time as inevitable precondition for successful logistics management.
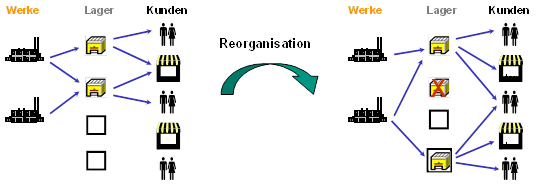
One distinguishes the following facility location problems:
- Planar (also: continuous) facility location problems
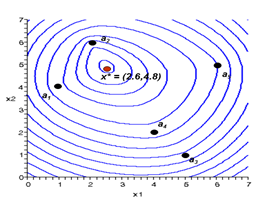
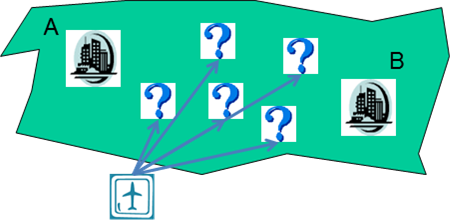
optimal facility location x, having five customers
- Facility location problems on networks
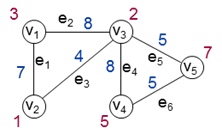
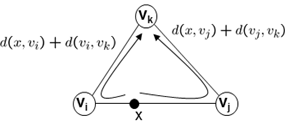
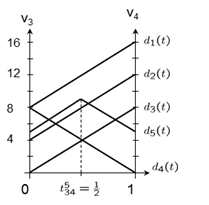
Left: Network with 5 customers (nodes), weights of the nodes describe the customers' demands, distances between the nodes are denoted as the weights of the edges. Middle: At the bottleneck point x, the distance via the left node equals the one via the right node. Right: Distance function of an arbitrary point on the edge between nodes 4 and 5.
- Discrete facility location problems
Shutdown of an old warehouse and open one at a more advantageous location.
Ordered Median
Choosing the most suitable objective function is one of the biggest challenges in mathematically modeling facility location problems. The „ordered median function“ offers a new approach of covering many well known objective functions like minisum, minimax, cent-dian, k-centra as special cases all at once. In contrast to the classical approaches, this function is defined pointwise and especially for the continuous case not necessarily convex.
Example for a minisum problem: Find the optimal facility location for a new airport which minimizes the weighted sum of the distances to the potential catchment areas.
Example for minimax: Positioning of emergency service facilities to minimize the maximal distance to a potential emergency.
This new approach permits developing a much more uniform, standardized facility location theory than is state of the art in books and essays today. Further it is closer to practitioners' needs with respect to modeling the objective function. Ordered Median functions can be formulated for continuous facility location problems as well as facility location problems on networks and discrete facility location problems.
Stochastic Supply Network Design
Structuring a global supply chain is a complex decision making process. The complexity arises from the need to integrate several decisions, each with a relevant contribution to the performance of the whole system.
In such problems, the typical input includes a set of markets, a set of products to be manufactured and/or distributed, demand forecasts for the different markets and some information about future conditions (e.g. production and transportation costs).
Making use of the above information, companies must decide where facilities (e.g. plants, distribution centers) should be set operating, how to allocate procurement/production activities to the different facilities, and how to plan the transportation of products through the supply chain network in order to satisfy customer demands. Often, the objective considered is the minimization of the costs for building and operating the network.
Historically, researchers have focused relatively early on the design of production and distribution systems (see Geoffrion and Powers (1995)). Typically, discrete facility location models were proposed which possibly included some additional features but that still had a limited scope and were not able to deal with many realistic supply chain requirements.
However, in the last decade, much research has been done to progressively develop more comprehensive (but tractable) models that can better capture the essence of many supply chain network design (SCND) problems and therefore become a useful tool in the decision making process. This can be seen in the papers by Melon et al. (2009) and Shapiro (2004), where it also becomes clear that many aspects of practical relevance in supply chain management (SCM) are still far from being fully integrated in the models existing in the literature.
As pointed out by Shapiro (2004), in corporate planning, financial decisions may strongly interact with the supply chain planning. In fact, structuring and managing a supply chain is often just part of a whole set of activities associated with a company. Accordingly, the investments in the supply chain must be integrated with other profitable investments.
Usually, a supply chain network has to be in use for some time meanwhile the underlying conditions may change. In some situations, a single-period facility location model may be enough to find a robust network design. However, in most cases, it is possible and even desirable to allow a change in the decisions in order to better absorb the changes in the parameters and thus to adjust the system accordingly. In such cases there is typically a discrete set of points in time in which changes can be made in the network structure.
Another feature that can hardly be avoided in many SCND problems regards the uncertainty associated to the future conditions which may influence the input of the problem, and the need to include this uncertainty in the models supporting the decision making process. Different sources of uncertainty exist that can be included in the models (see Snyder (2006)) such as demand, production or distribution costs, supply of raw materials etc. The uncertainty existing in the data leads to the need to find robust SCND decisions and/or consider ways for measuring and optimizing the risk associated with those decisions.
A constraint often considered in the literature devoted to SCND problems is that all the demand must be supplied throughout the planning horizon. However, for several reasons such constraint may become meaningless. Firstly, the demand is uncertain. Secondly, due to the existence of other investments in alternative to those that can be made in the supply chain, the company may prefer not to invest in a supply chain the amount needed to assure the complete demand satisfaction. Taking these arguments into consideration, a more interesting and from a practical point of view more reasonable alternative is to measure the service level (e.g. the proportion of satisfied demand) and to reward it in the objective function.
We are the first one which discusses a SCND problem capturing all the above mentioned aspects. We consider a supply chain network design problem with multiple periods, stochasticity and risk. The planning horizon is divided into several time periods in each of which several decisions can be made namely,
- the facilities that should be operating and thus the investments to make in the supply chain structure,
- other investments to make in addition to the previous ones,
- the loans to get and
- the flow of commodities through the network.
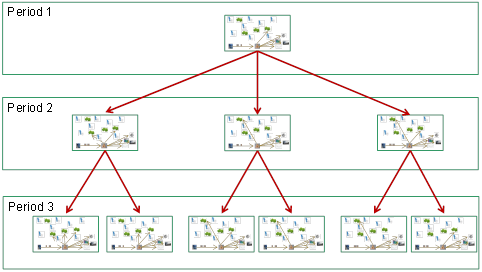
This scenario tree describes a facility location problem with three periods. There are three possible states in period 2 and two in period 3.
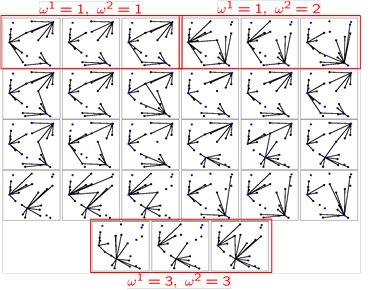
Stochasticity is considered for the demand and for the interest rates. The uncertainty is described by a set of scenarios. Revenues are included in the model as well as the ROI. The service level for each customer is calculated and weighted in the objective function. Finally, a measure of risk is introduced. The objective is to minimize the overall cost which is evaluated considering the investments made, the revenues, and the transportation costs. Thereby we search for the optimal decision for all the potential states in a scenario tree.
Optimal location and allocation decisions for the third period in a scenario tree with 3 potential realisations in each period (27 scenarios).
Contact persons